In the quarter turn metric, any move takes a local maximum to a position that is one move closer to Start. In the face turn metric, a move may take a local maximum to a position that is one move closer to Start or to a position that is the same distance from Start.
A strong local maximum in the face turn metric is a position from which all 18 face moves take the Cube one move closer to Start. A local maximum in the face turn metric that is not a strong local maximum is a weak local maximum. Most local maxima in the face turn metric seem to be weak local maxima. I'm not aware of any theoretical reason why strong local maxima must exist in the face turn metric, but a search of Cube space reveals that they do. Here follow the two shortest such positions. They were discovered by Jerry Bryan.
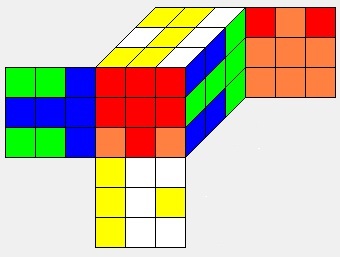 D2 F2 L2 D' U L2 F2 D' U' (9f*)
D2 F2 L2 D' U L2 F2 D' U' (9f*)
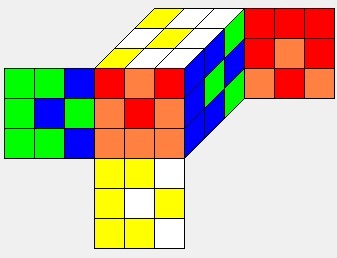 U2 B2 L2 D U' R2 B2 D' U' (9f*)
U2 B2 L2 D U' R2 B2 D' U' (9f*)